sin60的值，一个简单的数学概念与实际应用的结合

010sin0等于0，这个结论是根据正弦的定义得出来的。在直角三角形中，我们定义任意一锐角A的对边与斜边的比为A的正弦，记作sinA。按照这个定义，sinA=∠A的对边/斜边。由此我们可以得知，sin是正弦，表示对边与斜边的比。特别地，当角度为0度时，对应的对边长度为0，因此sin0=0。

1、我们还可以通过正弦函数的定理来理解这个结果。在一个三角形中，各边和它所对角的正弦的比相等，即a/sin A=b/sin B=c/sin C。这个定理可以帮助我们理解为什么sin90=1，因为当角度为90度时，对边与斜边的比就是1。

除了这些基本的性质，正弦函数还有许多重要的应用。例如，在三角形中，我们可以通过正弦函数来求面积。S△=c2sinAsinB/2sin(A+B)（S△为三角形的面积，三个角为∠A∠B∠C，对边分别为a,b,c）。

2、我们还要注意一些特殊角的三角函数值。例如，sin 0° = 0，cos 0° = 1，tan 0° = 0；sin 30° = 1/2，cos 30° = √3/2，tan 30° = √3/3；等等。这些特殊值在实际问题中经常用到。

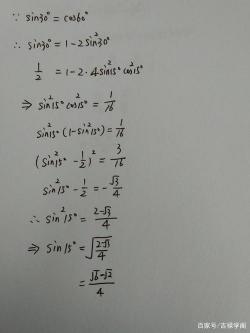
正弦函数是三角学中非常重要的概念之一，它有许多重要的性质和应用。通过掌握正弦函数的定义、性质和特殊值，我们可以更好地理解和应用它。