多普勒效应公式：揭示波长与频率的奥秘

多普勒效应是物理学中的一个重要概念，它描述了波源和观察者相对运动时，波长和频率的变化。这个效应最初由奥地利物理学家及数学家克里斯琴·约翰·多普勒于1842年提出，因此被命名为“多普勒效应”。

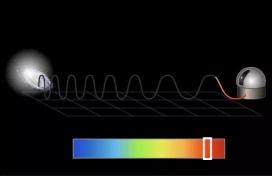
多普勒效应的基本原理是：当波源和观察者之间存在相对运动时，观测到的波长和频率会发生改变。具体来说，当观察者接近波源时，观测到的波长会变短，频率会升高；而当观察者远离波源时，观测到的波长会变长，频率会降低。这种变化程度与波源的速度有关，速度越高，效应越明显。

多普勒效应的公式表达为：f' = f * (1 + v/V) / (1 - u/V)。其中，v表示观察者相对于波源的速度，u表示波源相对于观察者的速度。当v>0或v<0时，表示观察者接近或远离波源；当u>0或u<0时，表示波源接近或远离观察者。

对于光波的多普勒效应，还需要考虑洛伦兹变化，公式为：f = ((c - v) / (c + v))^(1/2) * f。其中，c表示光速。

多普勒效应在天文学中有广泛的应用。自19世纪下半叶以来，天文学家就利用多普勒效应测量恒星的视向速度。如今，多普勒效应被广泛应用于测量天体和人造卫星的运动速度。

除了声波，多普勒效应还适用于所有类型的波，包括电磁波。科学家爱德文·哈勃使用多普勒效应得出了宇宙正在膨胀的结论。他发现远离银河系的天体发射的光线频率变低，即移向光谱的红端，称为红移。天体离开银河系的速度越快，红移越大，这说明这些天体在远离银河系。

多普勒效应是物理学中的一个重要概念，它描述了波源和观察者相对运动时波长和频率的变化。这个效应不仅仅适用于声波，还适用于所有类型的波，包括电磁波。通过理解和运用多普勒效应，我们可以更好地理解自然界的各种现象。