求解轨迹方程的四种方法：定义法、相关点法、参数法和直译法

如何求轨迹方程？有几种常见的方法可以应用

当我们需要求解一个物体的运动轨迹时，首先需要找到其轨迹方程。有多种方法可以帮助我们得到这个方程，下面将详细介绍四种常用的方法。

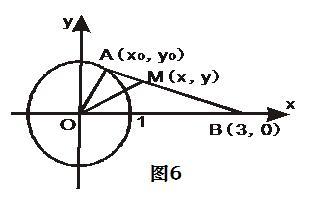
定义法：对于一些常见的轨迹，如椭圆和双曲线，我们可以直接根据它们的定义和性质来写出方程。这种方法简单直接，但只适用于已知轨迹形状的情况。

相关点法：这个方法的应用相当广泛。我们首先找出与所求轨迹相关的其他轨迹方程，然后通过这些方程之间的关系来推导出目标轨迹方程。这种方法需要细心分析，但能解决许多复杂的问题。

参数法：这是求轨迹方程中最简单的方法。只要知道两个点的坐标，我们就可以设置一个参数，然后通过这个参数来求解轨迹方程。这种方法直观易懂，适合初学者使用。

直译法：我们需要仔细阅读题目，明确题中所给的条件。然后，将这些条件翻译成数学方程，并联立这些方程来求解轨迹。这种方法需要一定的数学基础，但能帮助我们深入理解问题的本质。

这四种方法各有特点，可以根据具体问题的复杂性和需求选择合适的方法来求解轨迹方程。