相交弦定理的证明与推论：理解圆内线段比例和共圆性的关键

相交弦定理的证明

为了证明相交弦定理，我们首先需要连接线段AC和BD。

根据圆周角定理的推论，我们知道在同圆或等圆中，同(等)弧所对的圆周角是相等的。因此，我们可以得出∠A=∠D和∠C=∠B。

基于上述角度相等的关系，我们可以推断出△PAC与△PDB是相似的。这是由于三角形的相似性质，即当两个三角形的两组对应角相等时，这两个三角形是相似的。

由于△PAC与△PDB相似，我们可以得出比例关系：PA∶PD=PC∶PB。进一步地，我们可以得到乘积关系：PA·PB=PC·PD。

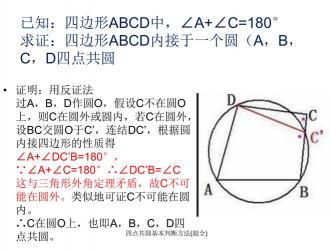
值得注意的是，相交弦定理的逆定理同样成立，它可以作为证明四边形是圆的内接四边形的方法。如果P点选在圆内任意一点，这个证明更具一般性。此外，逆定理也可以用于证明四个点共圆的情况。