反三角函数公式：基础概念与常用公式的总结

反三角函数，作为基本初等函数的一种，在数学中占据着重要的地位。它是包括反正弦arcsin x、反余弦arccos x、反正切arctan x、反余切arccot x、反正割arcsec x和反余割arccsc x等一系列函数的统称。

1、我们需要明白反三角函数的定义和性质。这些函数是正弦、余弦、正切等函数的反函数，意味着它们在特定的定义域内，将一个数值转换为其对应的角度。

常用反三角函数有一些基本的公式和定理，以下是其中一些重要的公式：

反正弦函数：arcsin(-x) = -arcsinx，arccos(-x) = π - arccosx，arctan(-x) = -arctanx，arccot(-x) = π - arccotx。

反余弦函数：y = cosx在[0, π]上的反函数，记作arccosx，表示一个余弦值为x的角。

反正切函数：正切函数y=tan x在(-π/2，π/2)上的反函数，记作arctanx，表示一个正切值为x的角。

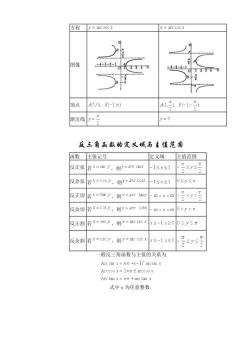
反余切函数：余切函数y=cot x在（0，π）上的反函数，记作arccotx，表示一个余切值为x的角。

反正割函数：正割函数y=sec x在[0,π/2)U(π/2,π]上的反函数，记作arcsecx，表示一个正割值为x的角。

反余割函数：余割函数y=csc x在[-π/2,0)U(0,π/2]上的反函数，记作arccscx，表示一个余割值为x的角。

2、还有一些重要的恒等式，如sin(arcsinx) = x，cos(arccosx) = x，tan(arctanx) = x等。

这些公式和定理不仅帮助我们理解反三角函数的性质，而且在实际问题中提供了有效的解决方法。无论是解决几何问题还是进行数值计算，反三角函数都是不可或缺的工具。

反三角函数作为数学中的重要部分，它的学习和理解对于深化数学知识体系、解决实际问题都具有重要意义。通过掌握这些基本的公式和定理，我们可以更好地理解和应用反三角函数。