乘方的运算法则与符号法则：理解并掌握乘方运算的关键

乘方的运算法则与符号法则

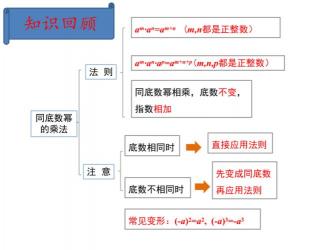
乘方的运算法则包括同底数幂法则、正整数指数幂法则、分数的乘方法则、积的乘方、同指数幂乘法、完全平方等。这些法则帮助我们理解和操作指数和幂运算。

同底数幂法则：当两个同底数的幂相乘或相除时，底数保持不变，指数则相加或相减。例如，a^m × a^n = a^(m+n) 和 a^m ÷ a^n = a^(m-n)。

正整数指数幂法则：这是描述如何通过连续乘以同一个数来得到幂的结果。例如，(a^k)^n = a^(kn)，其中k和n都是正整数。

平方差公式：这是一个特殊的乘方运算规则，表示两个数的和乘以它们的差等于它们的平方差。即，(a+b) × (a-b) = a^2 - b^2。

分数的乘方法则：当两个分数相乘时，它们的底数相除，指数相加。即，(a/b)^k = a^k/b^k。

幂的乘方法则：当一个幂再次被取幂时，底数保持不变，指数则相乘。即，(a^m)^n = a^(m×n)。

积的乘方：当一个积被取幂时，每个因数分别被取幂，然后将得到的指数相乘。即，(a×b)^n = a^n × b^n。

同指数幂乘法：当两个同指数的幂相乘时，指数保持不变，底数相乘。

完全平方：两个数的和（或差）的平方等于它们各自平方的和加上（或减去）它们的积的两倍。

有理数乘方的符号法则包括：

负数的偶次幂是正数，负数的奇数幂是负数。

正数的任何次幂都是正数。

0的任何正数次幂都是0。

这些运算法则和符号法则为我们提供了在数学中处理和解释乘方运算的工具和基础。