直角三角形：性质、判定方法和应用

直角三角形是几何学中的基本图形之一，它有一个角为直角，通常由两条直角边和一个斜边组成。根据勾股定理，直角三角形的两条直角边的平方和等于斜边的平方。直角三角形有许多特殊性质和判定方法，如它的内角和为180°，两锐角为45°等。

在直角三角形中，与直角相邻的两条边称为直角边，直角所对的边称为斜边。直角三角形直角所对的边也叫作“弦”。若两条直角边不一样长，短的那条边叫作“勾”，长的那条边叫作“股”。

等腰直角三角形是一种特殊的三角形，它具有所有三角形的性质，如具有稳定性、内角和为180°等。此外，等腰直角三角形的两直角边相等，两锐角为45°，斜边上中线、角平分线、垂线三线合一。等腰直角三角形斜边上的高为此三角形外接圆的半径R。

通过面积法，我们可以求出直角三角形斜边上的高。具体来说，如果两条直角边的长度分别为a和b，斜边长度为c，那么斜边上的高h可以通过以下公式求得：h = a × b ÷ c。这个公式在求解一些几何问题时非常有用。

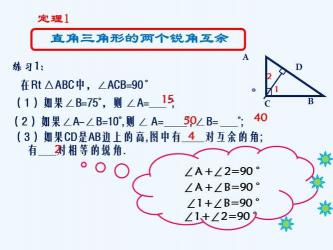
直角三角形是一个重要的几何图形，它在数学、物理和其他领域都有广泛的应用。通过了解它的性质和判定方法，我们可以更好地理解和应用这个图形。