等腰三角形面积计算方法：利用底和高或性质定理求解

在计算等腰三角形的面积时，我们可以通过一种简单的方法来计算。假设等腰直角三角形两腰分别为a和b，底为c，那么我们可以得到其面积为S=ab/2。由于等腰直角三角形的性质，底边c上的高h等于c/2。因此，三角形的面积也可以表示为S=ch/2=c^2/4。

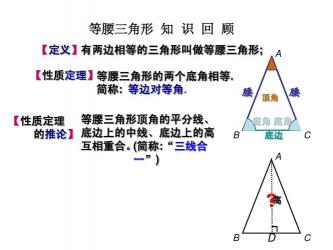
在解决等腰三角形问题时，有多种方法。我们可以使用三线合一的性质，这是等腰三角形中最重要的性质之一。所谓的三线，是指等腰三角形中的顶角角平分线、底边中线和底边的高线。这三条线必然是合一的。

1、我们还可以使用平行线法。这种方法一般是做一腰的平行线，从而得出两个角相等，再利用三角形全等的性质得出结果。

2、截长补短法或截长取短法也是解决等腰三角形问题的一种有效方法。就是在某一条线段上截取一条线段，使其等于已知线段。或者，延长某一线段，使其等于某已知线段。这种方法在解题中很常用，需要我们细心钻研，多探索和勤学苦练。

3、我们还可以使用加倍折半法或倍长中线法来求解等腰三角形的问题。这些方法都是基于三角形的性质和定理进行的。

等腰三角形的面积可以通过底和高来计算，也可以利用等腰三角形的性质进行求解。在解决等腰三角形的问题时，我们可以采用多种方法，如三线合一、平行线法、截长补短法、加倍折半法等。这些方法都需要我们熟练掌握三角形的性质和定理。