两直线垂直时斜率的奥秘

两条垂直的直线在相交时，它们的斜率乘积总是-1。斜率是描述直线或曲线切线相对于横坐标轴的倾斜程度。通常，它可以通过直线或曲线切线与横坐标轴之间的夹角正切值，或者通过两点纵坐标和横坐标的差值比来计算。

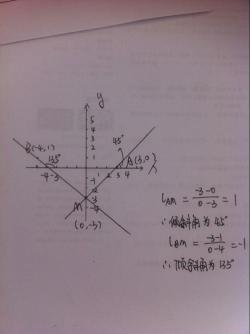
斜率也被称为“角系数”，它表示直线与横坐标轴正向之间的夹角正切值，用于量化直线对水平面的倾斜程度。当直线与x轴垂直时，它的斜率不存在，因为直角的正切值是无穷大。

在一次函数y=kx+b中，k代表函数图像的斜率。如果直线L的斜率存在，那么当x=0时，y=b。此外，点斜式y1-y2=k(x1-x2)也可用于描述直线上任意两点的斜率关系。

对于任意函数上的任意一点，其斜率等于其切线与x轴正方向所成角的正切值，也就是k=tanα。在公式ax+by+c=0中，斜率k可以通过-a/b来计算。