一元二次不等式：理解与解法详解

一元二次不等式是指含有一个未知数且未知数的最高次数为2的不等式，一般形式为ax²+bx+c>0或ax²+bx+c<0，其中a不等于0。不等式是用不等号（<，>，≥，≤，≠）连接的式子。

当a>0时，一元二次不等式的解的情况有：

判别式△(b²-4ac)>0时，有两个不相等的解。

判别式△(b²-4ac)=0时，因为a>0，二次函数图象抛物线的开口向上，抛物线与x轴有一个交点，则x₁=x₂，所以不等式ax²+bx+c>0的解集是x≠x1的全体实数，而不等式ax²+bx+c<0的解集是空集。

判别式△(b²-4ac)<0时，抛物线在x轴的上方与x轴没有交点。所以不等式ax²+bx+c>0的解集是全体实数，而不等式ax²+bx+c<0的解是空集。

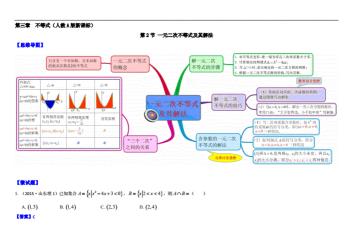
当a<0时，一元二次不等式的解的情况有：

判别式△(b²-4ac)>0时，有两个不相等的解。

判别式△(b²-4ac)=0时，因为a<0，二次函数图象抛物线的开口向下，抛物线与x轴有一个交点，则x₁=x₂，所以不等式ax²+bx+c<0的解集是x≠x1的全体实数，而不等式ax²+bx+c>0的解集是空集。

判别式△(b²-4ac)<0时，抛物线在x轴的下方与x轴没有交点。所以不等式ax²+bx+c<0的解集是全体实数，而不等式ax²+bx+c>0的解是空集。