轻松掌握！平方根表口诀与性质解析

在数学的广袤领域中，平方根是一个基础但至关重要的概念。如何快速准确地记忆平方根的相关知识和计算方法呢？今天，我们将为你提供一个实用的平方根口诀表，并深入解析平方根的性质，帮助你轻松掌握这一数学知识点。

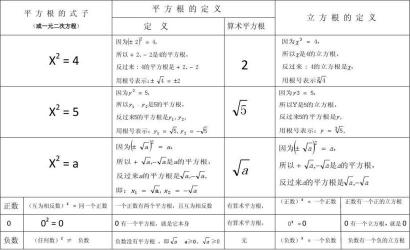
一、平方根口诀表

负数方根不能行，零取方根仍为零。

正数方根有两个，符号相反值相同。

2作根指可省略，其它务必要写明。

负数只有奇次根，算术方根零或正。

二、1到20的平方数口诀表

为了更直观地记忆平方数，我们为你整理了1到20的平方数口诀表：

1²=1、2²=4、3²=9、4²=16、5²=25、6²=36、7²=49、8²=64、9²=81、10²=100、11²=121、12²=144、13²=169、14²=196、15²=225、16²=256、17²=289、18²=324、19²=361、20²=400。

三、平方根的性质解析

一个正数如果有平方根，那么必定有两个，它们互为相反数。显然，如果我们知道了这两个平方根的一个，那么就可以及时地根据相反数的概念得到它的另一个平方根。

如果一个正数x的平方等于a，即x的平方等于a，那么这个正数x叫做a的算术平方根。a的算术平方根记为“根号a”，a叫做被开方数。

规定：0的平方根是0。

负数在实数范围内不能开平方，只有在复数范围内，才可以开平方根。例如：-1的平方根为±i，-9的平方根为±3i。

平方根包含了算术平方根，算术平方根是平方根中的一种。平方根和算术平方根都只有非负数才有。被开方数是乘方运算里的幂。求平方根可通过逆运算平方来求。开平方：求一个非负数a的平方根的运算叫做开平方，其中a叫做被开方数。若x的平方等于a，那么x就叫做a的平方根，即正负根号a等于正负x。

通过以上的口诀表和性质解析，我们希望能帮助你在数学学习中更轻松地掌握平方根的相关知识和计算方法。记住这些口诀和性质，将使你在解决数学问题时事半功倍。