空集符号的含义与使用

数学符号与集合的分类

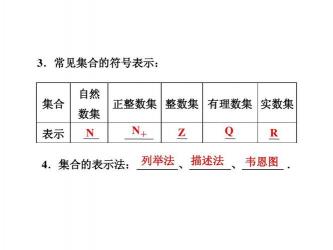
数学集合符号有许多种，它们分别代表了不同的集合类别。以下是一些常见的数学集合符号及其名称：

N：非负整数集合或自然数集合 {0, 1, 2, 3, …}

N* 或 N+：正整数集合 {1, 2, 3, …}

Z：整数集合 {…, -1, 0, 1, …}

Q：有理数集合

Q+：正有理数集合

Q-：负有理数集合

R：实数集合（包括有理数和无理数）

R+：正实数集合

R-：负实数集合

C：复数集合

∅：空集（不含有任何元素的集合）

1、数学集合之间还可以进行多种运算，如交集、并集、补集等。这些运算可以满足如下的运算律：

集合交换律：A∩B=B∩A；A∪B=B∪A。

集合结合律：(A∩B)∩C=A∩(B∩C)；(A∪B)∪C=A∪(B∪C)。

集合分配律：A∩(B∪C)=(A∩B)∪(A∩C)；A∪(B∩C)=(A∪B)∩(A∪C)。

数学集合的表示方法主要有以下几种：

列举法：把集合中的元素一一列举出来，并用花括号括起来表示集合的方法叫列举法。

描述法：用集合所含元素的共同特征表示集合的方法，称为描述法。

文氏图法：画一条封闭的曲线，用它的内部来表示一个集合。

根据集合所含元素的数量，可以分为无限集和有限集。无限集是指含有无限个元素的集合，如N（自然数集）、R（实数集）等。有限集则是指含有有限个元素的集合，如Nn={1，2，3，……，n}。