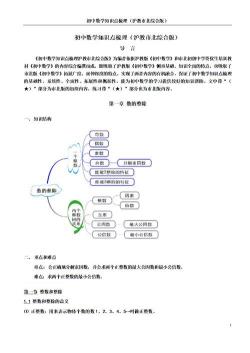
整除的定义和性质：理解整数之间的关系

整除是数学中的一个重要概念，指的是整数a除以非零整数b，商为整数，且余数为零。这种情况下，我们说a能被b整除（或说b能整除a），a为被除数，b为除数，即b/a，读作“b整除a”或“a能被b整除”。a叫做b的倍数，b叫做a的约数（或因数）。整除属于除尽的一种特殊情况。

整除有一些重要的性质。如果a/b和a/c都是整数，那么a可以除以b和c的积，即a/(b±c)。如果a/b是整数，那么对任意非零整数c，a可以除以bc。第三，对于任意非零整数a，±a/a都是±1。第四，如果a/b和b/a都是整数，那么|a|=|b|。第五，如果a能被b整除，c是任意整数，那么积ac也能被b整除。第六，如果a同时被b与c整除，并且b与c互质，那么a一定能被积bc整除，反过来也成立。

1、对于任意整数a和正整数b，总存在唯一的数对q和r，使得a=bq+r，其中0≤r<b。这个事实被称为带余除法定理，是整除理论的基础。

这些性质在数学和算术中都有广泛的应用，可以帮助我们更好地理解和处理整数之间的关系。