初二数学一次函数：定义、区别与解题技巧

初二数学一次函数经典例题及解题技巧

一、一次函数与正比例函数的定义与区别

一次函数：一般地，形如y=kx+b（其中k、b为常数且k≠0）的函数称为一次函数。

正比例函数：当b=0，k≠0时，y=kx，则y是x的正比例函数。

一次函数与正比例函数的区别与联系：

从解析式看，y=kx+b（k≠0，b≠0）是一次函数，而y=kx（k≠0，b=0）是正比例函数。正比例函数是一次函数的特例，一次函数是正比例函数的推广。

从图象看，y=kx（k≠0）是过（0，0）点的一条直线，而y=kx+b（k≠0）是过（0，b）点且与y=kx平行的一条直线。

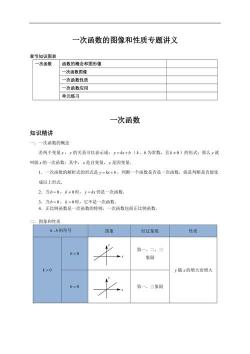
二、k、b的符号与一次函数图象的位置关系

当k>0时，图象经过一、三象限，y随x的增大而增大；

当k<0时，图象经过二、四象限，y随x的增大而减小。

当b>0时，图象与y轴的交点在x轴的上方；

当b=0时，图象与y轴的交点在原点；

当b<0时，图象与y轴的交点在x轴的下方。

三、确定一次函数与正比例函数的条件

正比例函数y=kx（k≠0）中的待定系数为k，因此确定正比例函数只需一个条件。

一次函数y=kx+b（k≠0）中的待定系数为k和b，因此确定一次函数需两个条件。从几何意义考虑：正比例函数的图象是过（0，0）点，而“两点确定一条直线”，因此只需再知另一点即可，而一次函数必需知两点。

四、解题技巧

根据已知条件求解析式。

根据题意列出方程解决问题。

注意取值范围的实际应用问题。

以上就是初二数学一次函数的经典例题及解题技巧，希望能帮助到大家！