奇变偶不变符号看象限-三角函数诱导公式的口诀及应用

三角函数的诱导公式是三角函数中重要的恒等式，它允许我们将角度较大的三角函数转换为角度较小的三角函数。这些公式在解决三角函数问题时非常有用，可以帮助我们简化计算并找到解决方案。

公式一：终边相同的角的同一三角函数的值相等

设α为任意锐角，弧度制下的角的表示：sin(2kπ+α)=sinα(k∈Z)cos(2kπ+α)=cosα(k∈Z)tan(2kπ+α)=tanα(k∈Z)cot(2kπ+α)=cotα(k∈Z)

公式二：π+α的三角函数值与α的三角函数值之间的关系

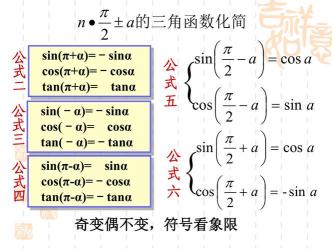
设α为任意角，弧度制下的角的表示：sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα

公式三：任意角α与 -α的三角函数值之间的关系

sin(-α)=-sinacos(-α)=cosatan(-α)=-tanacot(-α)=-cot

公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系

sin(π-α)=sinacos(π-α)=-cosatan(π-α)=-tanacot(π-α)=-cot

公式五：利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系

sin(2π-α)=-sinacos(2π-α)=cosatan(2π-α)=-tanacot(2π-α)=-cot

公式六：(1) π/2+α与α的三角函数值之间的关系

sin(π/2+α)=cosacos(π/2+α)=-sinatan(π/2+α)=-cotacot(π/2+α)=-tan

(2) π/2-α与α的三角函数值之间的关系

sin(π/2-α)=cosacos(π/2-α)=sinatan(π/2-α)=cotacot(π/2-α)=tan

(3) 3π/2+α的三角函数值之间的关系

sin(3π/2+α)=-cosacos(3π/2+α)=sinatan(3π/2+α)=-cotacot(3π/2+α)=-tan

(4) 3π/2-α的三角函数值之间的关系

sin(3π/2-α)=-cosacos(3π/2-α)=-sinatan(3π/2-α)=cotacot(3π/2-α)=tan

这些公式在解决三角函数问题时非常有用，可以帮助我们简化计算并找到解决方案。