三角函数降幂公式：简化平方项的重要工具

三角函数在高中数学中的重要性和难度显而易见，其抽象性和概念性也需要学生深入理解和掌握。尤其在三角函数的解题过程中，学生容易在细节上出错。为了帮助学生更好地掌握三角函数，本文整理了三角函数的升幂公式、降幂公式、二倍角公式、半角公式等，供大家参考。

升幂公式是三角函数中常用的公式之一，可以将三角函数的指数进行化简。例如，sinx=2sin(x/2)cos(x/2)，cosx=2cos^2(x/2)-1=1-2sin^2(x/2)=cos^2(x/2)-sin^2(X/2)，tanx=2tan(x/2)/[1-tan^2(x/2)]。

降幂公式则是将三角函数的平方项进行化简，例如cos²x=(1+cos2x)/2，sin²x=(1-cos2x)/2，tan²x= sin²x / cos²x=(1-cos2x)/(1+cos2x)。

二倍角公式将三角函数中的角度放大两倍，从而得到一些常见的三角函数值。例如，sin2x=2sinxcosx，cos2x=(cosx)^2-(sinx)^2=2(cosx)^2-1=1-2(sinx)^2。

半角公式则是将角度缩小一半，从而得到一些常见的三角函数值。例如，sin(A/2)=√((1-cosA)/2)，cos(A/2)=√((1+cosA)/2)，tan(A/2)=√((1-cosA)/((1+cosA))。

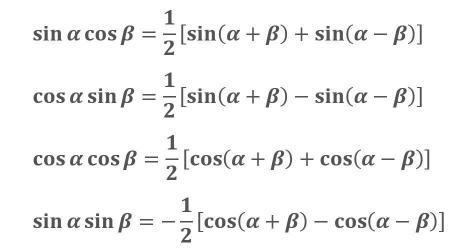
通过掌握这些公式，学生可以更轻松地解决三角函数的习题解答过程中的问题。同时，这些公式也是学习其他数学知识的基础，例如在学习微积分、复数等知识时都需要用到这些公式。因此，学生应该认真掌握这些公式，为以后的学习打下坚实的基础。