轻松掌握：一次函数奇偶性判断方法与实例解析

一次函数的奇偶性

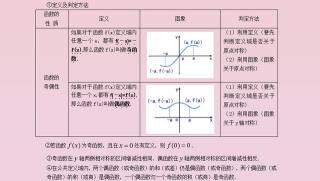
一次函数的奇偶性是指，当函数y=kx+b中的b不等于0时，该函数既不是奇函数也不是偶函数；而当b等于0时，该函数为奇函数。奇函数的特点是关于原点对称，而偶函数的特点是关于y轴对称。

要判断一个函数的奇偶性，首先要看其定义域是否关于y轴或原点对称。如果定义域不满足这些条件，那么该函数就既不是奇函数也不是偶函数。对于一次函数来说，其定义域为实数集，因此可以判断其奇偶性。

判断函数的奇偶性的方法是：

假设任意函数为y(x)。

将x替换为−x，得到y(−x)的表达式。

整合y(−x)的计算结果，判断其是否等于−y(x)或y(x)。

如果y(−x)=−y(x)，则该函数为奇函数。

如果y(−x)=y(x)，则该函数为偶函数。

如果y(−x)≈y(x)且y(−x)≈−y(x)，则该函数为非奇非偶函数。这种函数既不关于原点对称也不关于y轴对称。