三角函数中的正切公式：基本形式和应用

三角函数正切公式有哪些

三角函数是数学学习的重点，其中正切函数是三角函数的重要组成部分。那么，三角函数正切公式有哪些呢？下面和小编一起来了解一下吧！

常用正切公式

tan(a+b)=(tana+tanb)/(1-tana*tanb)

注：若是a-b则把后面的加减都换一下

1/tanb=cotb（这个公式不常用，偶尔用我们也经常写成正切的倒数的形式，不过选择题中会出现）

tanB=q（常数）则角B=acttan(q)这是反函数的公式。

常用公式整理

和角公式：sin(α+β)=sin(α)cos(β)+cos(α)sin(β)，sin(α+β)=sin(α)cos(β)+cos(α)sin(β)，cos(α+β)=cos(α)cos(β)−sin(α)sin(β)，cos(α+β)=cos(α)cos(β)−sin(α)sin(β)。

差角公式：sin(α−β)=sin(α)cos(β)−cos(α)sin(β)，sin(α−β)=sin(α)cos(β)−cos(α)sin(β)，cos(α−β)=cos(α)cos(β)+sin(α)sin(β)，cos(α−β)=cos(α)cos(β)+sin(α)sin(β)。

倒数关系：tanα·cotα=1，sinα·cscα=1，cosα·secα=1。

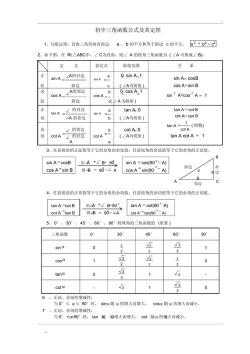
商的关系：sinα/cosα=tanα=secα/cscα，cosα/sinα=cotα=cscα/secα。

平方关系：sin^2(α)+cos^2(α)=1，1+tan^2(α)=sec^2(α)，1+cot^2(α)=csc^2(α)。

以上是三角函数正切公式的常见形式，希望对大家有所帮助。在学习三角函数时，需要掌握这些基本公式，以便更好地理解和应用它们。