π是不是有理数？答案是无理数

π不是有理数，而是无理数

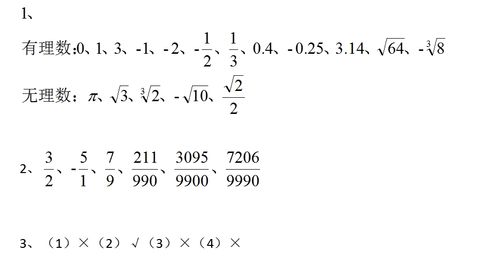
我们知道，有理数是可以表示为两个整数的比值，即有理数是一个整数a和一个正整数b的比，例如3/8，通则为a/b。有理数是整数和分数的集合，整数也可看做是分母为一的分数。有理数的小数部分是有限或为无限循环的数。然而，π=3.1415926...是无限不循环小数，这意味着它不能被表示为两个整数的比值。因此，π不属于有理数的范围。

事实上，π是一个无理数。无理数是指不能写作两整数之比的数，例如π和根号2等。它们的小数部分是无限不循环的，不能被表达为有限的小数。在位置数字系统中表示无理数时，它们不会终止，也不会重复，即不包含数字的子序列。这是无理数的一个显著特性，使得它们在许多数学领域中具有独特的性质和用途。

由于π是无限不循环小数，它不能被表示为两个整数的比值，因此被归类为无理数。这使得π在数学领域中具有独特的地位和重要性。