sin30度：特殊角度下的三角函数值及其推导

我们来看一下三角函数sin30°的值及推导过程。

已知角度为：30°

根据三角函数表，可知sin30°的值为：0.5

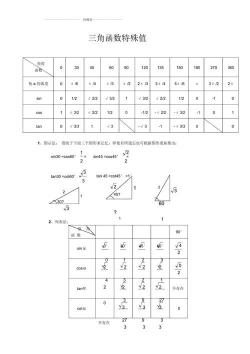
现在，我们来看一下具体的推导过程。

在正三角形ABC中，画一条高为AD，三角形ABC等腰三角形，D是BC中点，且AD平分∠A，∠BAD=30°。

根据三角函数的定义，sin30°=sinBAD=BD/AB。

由于BD=AB/2，所以sin30°=BD/AB=1/2。

所以，sin30°的值为0.5。

1、我们还可以根据三角函数的变化规律，来推断其他角度的三角函数值。

正弦值在[2kπ-π/2, 2kπ+π/2] (k∈Z)随角度增大（减小）而增大（减小），在[2kπ+π/2, 2kπ+3π/2] (k∈Z)随角度增大（减小）而减小（增大）；

余弦值[2kπ-π/2, 2kπ] (k∈Z)在随角度增大（减小）而增大（减小），在[2kπ, 2kπ+π] (k∈Z)随角度增大（减小）而减小（增大）；

正切值在[kπ, kπ+π/2] (k∈Z)随角度增大（减小）而增大（减小）。

因此，我们可以根据这些规律，来推断其他角度的三角函数值。