勾股定律：几何与代数的交汇点

勾股定理，一个简单而深远的数学概念，不仅在中考数学中占据重要地位，更是我们进一步探索几何、代数，乃至更高级数学领域的关键工具。它的公式简洁明了：a² + b² = c²，其中a和b是直角三角形的两条直角边，c是斜边。这个公式用代数语言阐述了几何形状——直角三角形的本质属性，是数形结合思想的典范。

勾股定理的逆定理同样重要，它告诉我们：如果三角形的三边长a，b，c满足a² + b² = c²，那么这个三角形必定是直角三角形，其中c为斜边。这一逆定理的存在，使得我们可以轻松地通过三边长来判断一个三角形是否为直角三角形。

特别值得注意的是，有些正整数组合（如3、4、5或6、8、10等）满足勾股定理的条件，我们称之为“勾股数”。熟悉这些常见的勾股数，可以在解决相关问题时大大提高效率。

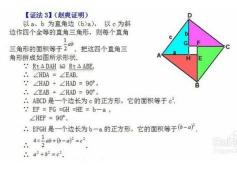
勾股定理的证明方法多种多样，已知的超过500种，这使其成为数学定理中证明方法最多的定理之一。其中，拼图法、青朱出入图和欧几里得证法都是极具代表性的证明方法，它们运用了不同的数学思想和技巧，但都殊途同归，验证了勾股定理的正确性。

拼图法通过割补拼接图形，利用面积不变原理推导出勾股定理。青朱出入图则是我国古代数学家刘徽提出的证明方法，它巧妙地运用数形结合思想，通过朱方和青方的互补关系证明勾股定理。而欧几里得证法则采用了严格的逻辑推理和辅助线构造，给出了一个基于三角形和正方形性质的证明。

勾股定理及其相关知识和证明方法不仅在数学考试中有着广泛应用，更是我们理解数学、探索数学世界的重要工具。