二元一次方程的解法：代入消元法与加减消元法的详细解析

解二元一次方程组的基本思路是“消元”。消元就是通过减少未知数的个数，将多元方程转化为一元一次方程，再求解未知数。解二元一次方程组主要有两种方法：代入消元法和加减消元法。

代入消元法是将方程组中的一个方程的某个未知数用含有另一个未知数的代数式表示出来，然后代入另一个方程中，消去一个未知数，得到一个一元一次方程。这种方法的关键是选取一个系数较简单的二元一次方程进行变形，用含有一个未知数的代数式表示另一个未知数，然后将变形后的方程代入另一个方程中消元。最后解这个一元一次方程，求出未知数的值，再将求得的未知数的值代入原方程组中的任何一个方程中，求出另一个未知数的值。

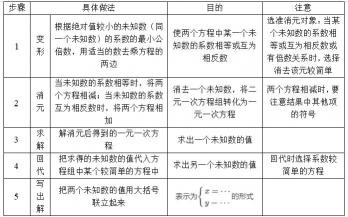
加减消元法则是当方程中两个方程的某一未知数的系数相等或互为相反数时，把这两个方程的两边相加或相减来消去这个未知数，从而将二元一次方程化为一元一次方程。这种方法的关键是利用等式的基本性质，将原方程组中某个未知数的系数化成相等或相反数的形式，然后相加或相减消元。最后解这个一元一次方程，求出未知数的值，再将求得的未知数的值代入原方程组中的任何一个方程中，求出另一个未知数的值。

这两种方法都是将二元一次方程组化为一元一次方程求解，但是适用的情况和具体的操作步骤有所不同。在使用时需要根据具体情况选择合适的方法。