几何体分类详解：柱体、锥体、球体及其他

几何体分类

几何体是立体几何中的基本单元，可以根据不同的特征进行分类。一般来说，几何体可以分为柱体、锥体和球体三类。柱体包括圆柱和棱柱，棱柱又可分为直棱柱和斜棱柱，棱柱体按底面边数的多少又可分为三棱柱、四棱柱、N棱柱。锥体包括圆锥体和棱锥体，棱锥分为三棱锥、四棱锥以及N棱锥。此外，还有旋转体，包括圆柱、圆台、圆锥、球、球冠、弓环、圆环、堤环、扇环、枣核形等。

平面几何图形

除了立体几何图形外，还有一些平面几何图形，如圆形、多边形和弓形等。圆形包括正圆、椭圆、多焦点圆和卵圆。多边形包括三角形、四边形、五边形、六边形等。弓形是由直线和圆弧构成的图形，包括优弧弓、劣弧弓、抛物线弓等。

几何体的结构特征

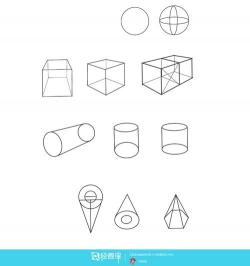
几何体有两个面互相平行，其余各面都是四边形，且每相邻两个四边形的公共边都互相平行。根据底面多边形的边数，可以将几何体分为三棱柱、四棱柱、五棱柱等。这些几何体的侧面、对角面都是平行四边形，侧棱平行且相等。平行于底面的截面是与底面全等的多边形。

立体几何计算方法与技巧

在立体几何中，有些问题需要计算点到直线的距离、两条异面直线间的距离以及点到平面的距离。求点到直线的距离时，经常应用三垂线定理作出点到直线的垂线，然后在相关的三角形中求解。求两条异面直线间的距离时，一般先找出其公垂线，然后求其公垂线段的长。求点到平面的距离时，一般找出过此点与已知平面垂直的平面，利用面面垂直的性质过该点作出平面的垂线，进而计算。也可以利用“三棱锥体积法”直接求距离。

以上信息仅供参考，如有需要，建议查阅相关网站。