圆柱的体积教案：从推导到应用，深入理解与实践

教学内容概览：

本次教学主要涵盖九年义务教育六年制第十二册第36～37页的内容，特别是例4、例5以及相关的练习题目。我们的目标是让学生掌握圆柱体积的计算方法，并理解其背后的推导过程。

教学目标：

深入掌握圆柱体积的计算公式，并能准确计算圆柱体的体积。

培养学生的迁移能力、逻辑思维能力和空间想象力。

引导学生通过实际问题和情境，体验数学中的转化思想和极限思想。

教学重点与难点：

教学的重点是圆柱体体积的计算，而难点则在于理解圆柱体体积公式的推导过程。

教学准备：

为了帮助学生更好地理解，我们将使用多媒体课件、圆柱形容器、水以及橡皮泥作为教学辅助工具。

教学过程：

一、导入新课

通过展示一个装有水的圆柱形容器，激发学生的好奇心。询问学生如何计算这些水的体积，引导学生思考解决问题的不同方法。

二、探索圆柱体积的计算方法

提出问题：对于形状各异的圆柱体，我们如何计算其体积呢？是否有一种通用的方法？

小组讨论：让学生分组讨论，探索计算圆柱体积的可能方法。

动手操作：提供圆柱体形状的橡皮泥，让学生尝试将其转化为长方体或正方体，从而计算其体积。引导学生思考这种方法的局限性。

三、推导圆柱体积公式

启发思考：引导学生思考如何将圆柱体转化为长方体，以便利用已知的长方体体积公式来求解。

演示推导：通过多媒体课件展示圆柱体转化为长方体的过程，让学生观察并理解这一过程中的变化。

公式根据长方体的体积公式，推导出圆柱体的体积公式：V = Sh（体积等于底面积乘以高）。

四、巩固练习与应用

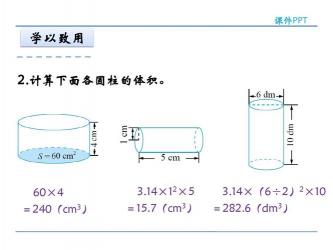
通过例4和例5的练习，让学生运用圆柱体积公式进行计算，并加深对公式的理解。

提供实际问题的情境，如计算人民大会堂门柱或压路机大前轮的体积，让学生将所学知识应用于实际生活中。

五、拓展延伸

提出一个挑战性问题：如何从一个给定的长方体中加工出一个体积最大的圆柱体？引导学生思考并探索解决方案。

六、课堂总结

回顾本节课的学习内容，让学生分享自己的收获和体会。强调圆柱体积公式的重要性以及在实际问题中的应用价值。

通过以上教学过程，我们希望能够帮助学生深入理解圆柱体积的计算方法，并培养他们的逻辑思维能力和空间想象力。同时，通过实际问题的应用，让学生感受到数学在生活中的实用性和趣味性。