e的x次方求导：揭秘其导数背后的数学奥秘

导数的求导法则详解

当我们面对由基本函数通过加、减、乘、除或复合运算构成的复杂函数时，如何求出其导函数呢？这时，我们需要运用一系列基本且实用的求导法则。以下是几个关键的求导法则，它们将帮助我们轻松应对各种求导挑战。

1、我们来谈谈线性组合的求导法则。如果一个函数是由几个基本函数的线性组合而成，那么我们可以分别对这几个基本函数求导，然后再将得到的导数进行线性组合。这一法则的核心思想在于“分别求导，再线性组合”。

2、我们来看两个函数乘积的求导法则。这个法则告诉我们，两个函数乘积的导数等于第一个函数的导数乘以第二个函数，再加上第一个函数乘以第二个函数的导数。这个法则可以用一个简单的公式来表示：“一导乘二+一乘二导”。

除了乘积的求导法则外，还有商的求导法则。当我们面对两个函数的商时，其导数的求解稍微复杂一些。具体来说，商的导数等于分子函数的导数乘以分母函数，再减去分子函数乘以分母函数的导数，最后将整个结果除以分母函数的平方。这个法则可以用一个公式来概括：“（子导乘母-子乘母导）除以母平方”。

3、当遇到复合函数时，我们需要使用链式法则来求导。链式法则是一种非常实用的方法，它允许我们逐层拆解复合函数，并分别求出每一层的导数。通过这种方法，我们可以轻松地找到复杂复合函数的导数。

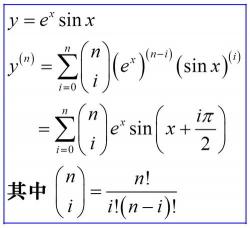
掌握这些基本的求导法则对于理解和应用导数至关重要。无论是处理线性组合、乘积、商还是复合函数，我们都可以运用相应的法则来轻松求解其导数。这些法则不仅简化了求导过程，还帮助我们更深入地理解导数的本质和应用。