三角形中心揭秘：什么是三角形的“重心”？

三角形重心定理的深入解析

三角形重心定理是几何学中的一个重要定理，它揭示了三角形三条中线的一个重要性质。具体来说，三角形的三条中线不仅交于一点，而且这一点位于各中线的三分之二处（从顶点算起）。这一性质在三角形的研究中具有重要的应用价值。

为了证明这一定理，我们可以按照以下步骤进行：

1、我们设三角形ABC的三条中线分别为AD、BE和CF，其中D、E、F分别是BC、AC和AB的中点。我们的目标是证明AD、BE和CF三线交于一点，并且这一点与顶点的距离等于它与对边中点的距离的两倍。

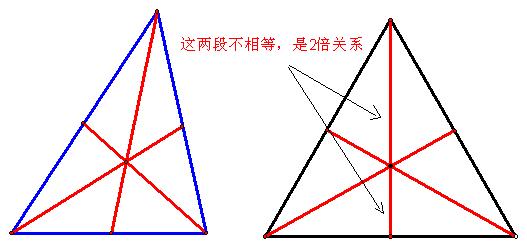
为了证明这一点，我们可以设BE与CF交于G点，并连结EF。由于EF是中位线，根据中位线的性质，我们知道EF与BC平行，并且EF的长度是BC的一半。

2、我们观察三角形EFG与三角形BCG。由于EF与BC平行，并且EF是BC的一半，根据相似三角形的性质，我们可以得出三角形EFG与三角形BCG是相似的。

由于三角形EFG与三角形BCG相似，我们可以利用相似三角形的性质，推导出G点位于BE和CF的三分之二处。这意味着G点不仅是BE和CF的交点，而且它到顶点B和C的距离分别是它到对边中点E和F的距离的两倍。

我们证明了三角形重心定理的正确性。这一定理不仅揭示了三角形中线的一个重要性质，而且为我们进一步研究三角形的性质提供了有力的工具。