arccosx的导数：探索三角函数与导数之间的关系

导数，又称为导函数值，是微积分中的核心概念。它描述了函数在某一点附近的变化率，展现了一个函数在特定点的切线斜率。导数的存在基于极限的观念，即通过局部线性逼近的方式对函数进行近似。在现实应用中，例如运动学中的瞬时速度，导数提供了物体运动状态变化的精确描述。

并非所有函数都有导数，且一个函数在所有点上也不一定都有导数。如果一个函数在某一点上的导数存在，则称该函数在该点可导；否则，称为不可导。值得注意的是，可导的函数一定是连续的，而不连续的函数则一定不可导。

对于给定的可导函数f(x)，其导数f'(x)本身也是一个函数，我们称之为f(x)的导函数或简称导数。求导是一个寻找极限的过程，其四则运算法则来源于极限的四则运算法则。反之，已知的导函数也可以用来反求原来的函数，即不定积分的过程。

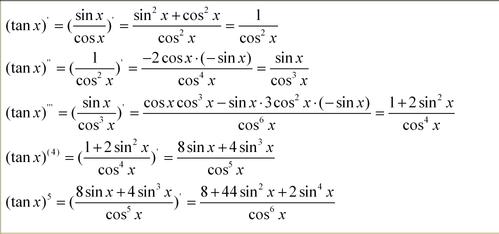
微积分基本定理揭示了求原函数与积分之间的等价关系。求导和积分作为微积分学中的基础概念，是一对互逆操作。深入理解导数的概念与应用，对于掌握微积分学以及解决实际问题具有重要意义。