定积分怎么求：从概念到应用的全面解析

定积分计算方法总结

定积分是数学中的一个重要概念，它涉及到对某一区间上的函数进行积分，以解决特定的问题。以下是关于定积分的总结，帮助你更好地理解这一概念。

一、定积分的概念

定积分是用来解决特定问题的积分运算，通常涉及到曲边梯形的面积、变速直线运动的路程等。通过定积分，我们可以分析函数的性质并解决实际问题。

二、定积分计算的充分条件

连续函数：如果函数在给定区间上连续，则该函数在该区间上可积。这是定积分的基本性质。

有界且间断点有限：如果函数在给定区间上有界，且只有有限个间断点，则该函数在该区间上也可积。

三、定积分的性质

非负性：如果函数在给定区间上非负，则其定积分也非负。即，∫abf（x）dx≥0。

可加性：如果函数在给定区间上被分为两部分，则其定积分也可以分为两部分相加。即，∫abf（x）dx=∫acf（x）dx+∫cbf（x）dx。

绝对值性质：|∫abf（x）dx|≤∫ab|f（x）|dx。这意味着函数的绝对值的积分不会超过该函数的积分。

积分中值定理：如果函数在给定区间上连续，则在积分区间内至少存在一个点ξ，使得∫abf（x）dx=f（ξ）（b—a）。这表明函数的积分等于函数在某个点上的值与区间长度的乘积。

四、定积分的应用

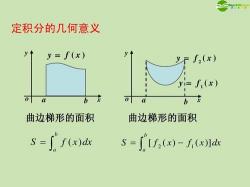
平面图形面积：定积分可以用来计算由曲线围成的面积，包括直角坐标系下和极坐标系下的面积计算。

旋转体体积：通过将连续曲线、直线及坐标轴所围成的面积绕坐标轴旋转，可以计算旋转体的体积。

立体体积：定积分还可以用来计算由平行截面面积已知的立体体积。

其他应用：定积分还可以应用于功、水压力、引力、函数的平均值等方面的计算。